Processingを用いて様々なシミュレーションを実施する上で最も大きな枠組みとして、数理モデルの作り方について解説します。数理モデルとは、現実の物理現象や社会現象を数学的に表現したモデルのことです。数理モデルの作成プロセスは以下のステップで進めることが一般的です。本記事における解説は抽象的な解説ですので、具体的な問題に対して数理モデルを構築したのちに再びこの記事を読まれると、記事の意味がさらによくわかると思います。
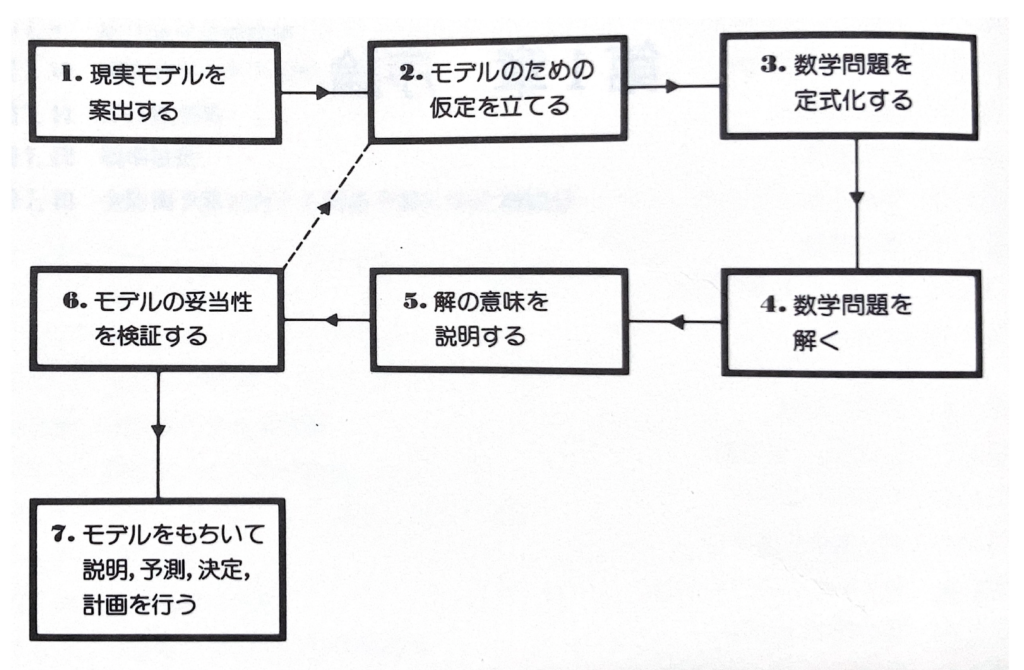
「微分方程式で数学モデルを作ろう」2p デヴィット・バージェス / モラグ・ボリー著 垣田 髙夫・大町 比佐栄 訳 より引用
目次
Step.1 現実モデルを案出する
※案出 : 工夫して考え出すこと
数理モデルを考える第一歩は、問題を定義することです。具体的には以下を行います。
- モデル化したい現象やプロセスを明確に定義します。
- 目的や目標を明確にし、何を求めるかを定義します。
Step.2 モデルのための仮定を立てる
モデル化を行うために対象となる現象やプロセスを単純化したり、仮定を追加したりします。どのような単純化や仮定をおいたかを明確にしておきます。
Step.3 数学問題を定式化する
重要な変数は何かを明らかにし、変数同士の関係を数式で表現します。この段階で現実の問題は何らかの数学的な問題に定式化されます。
Step.4 数学問題を解く
数学の様々なテクニックを用いて問題を解きます。このサイトでは、数学的な解を求めたり、数値計算による近似値の算出にチャンレンジします。
Step.5 解の意味を説明する
解としてもとめられた関数や数値を今度は現実モデルに対して、どういう意味と考えればいいのか解釈を行います。
Step.6 モデルの妥当性の検証
- モデルの予測が実際の観測データや経験と一致するか評価します。
- 不一致がある場合、仮定の再評価や新たなデータの収集、モデルの修正などが必要となります(Step.2へ戻る)
Step.7 モデルを用いて説明・予測・決定・計画を行う
- モデルを使用して、新しい洞察や予測を行います。
- モデルの適用範囲と限界を理解し、結果を適切に解釈します。
以上が数理モデルの作り方の概観になりますが、実際には様々な問題に対して数理モデルの作成と評価の経験を積み重ねる訓練が重要です。今後の記事では様々な問題を取り上げて数理モデルを作っていきます。
 Rikemen
Rikemen 

