Processingにおける回転・振動の実装 Part.2 極座標とデカルト座標

Part.1に続いて、Processingで回転や振動を扱うための数学やコードの書き方を解説していきます。今回は極座標とデカルト座標についてです。

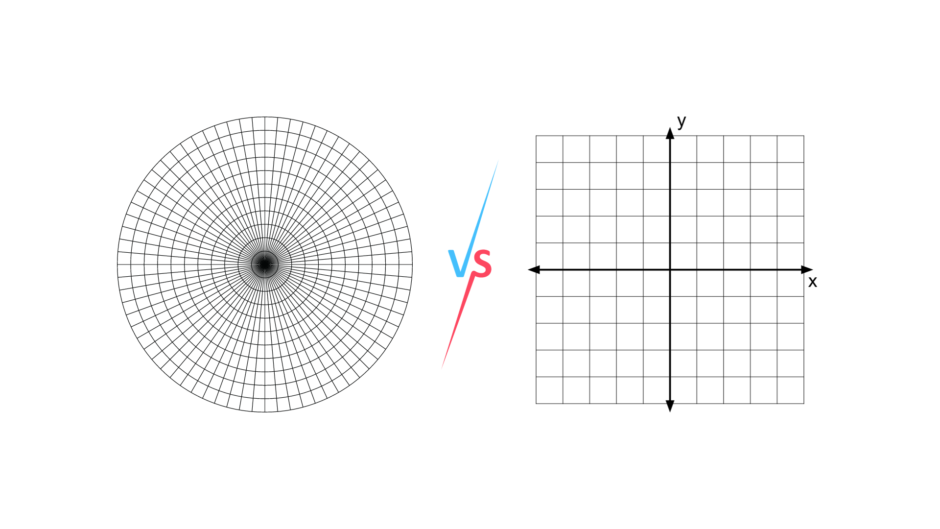
極座標とデカルト座標

デカルト座標系（直交座標系）: 平面上の任意の点を、原点からの水平および垂直方向への距離（x座標とy座標）によって表現します。

極座標系: 平面上の任意の点を、原点からの距離（半径 r）と、x軸の正の方向からの（角度θ）で表現します。

式と曲線24 ポイント — 「Try IT」「5分でわかる！極座標と直交座標(1)より引用

極座標の有効性

極座標系は、特に円や回転運動を表現する際に有効です。例えば、螺旋や放射状のパターンを描画する場合や、中心を中心とする対称性を持つ物体や現象を分析する際に、極座標系は自然で直感的な表現を提供します。

座標変換

極座標をデカルト座標に変換するためには、以下の関係式を使用します。 x=r⋅cos(θ)

y=r⋅sin(θ)

Processingにおける座標変換のコード例

以下は、Processingで極座標をデカルト座標に変換する簡単なコード例です。Processingでは極座標を直接取り扱う仕組みはないため、極座標で考えた値もデカルト座標の位置に変換して利用します。

float r = 100; // 半径
float theta = PI / 4; // 角度 (45度)

void setup() {
  size(200, 200);
  float x = r * cos(theta); // 極座標をデカルト座標に変換
  float y = r * sin(theta); // 極座標をデカルト座標に変換
  
//極座標を用いて、画面の中心を原点として半径100の円周上を12分割する円を描く

float r = 100; // 半径
float theta = 0; // 角度 (0度)
float delta_theta = TWO_PI / 12;

void setup() {
  size(300,300);


  background(255);
  translate(width / 2, height / 2); // 座標系の中心を画面の中心に移動
  for (int i = 0; i < 12; i ++) {
    theta = i * delta_theta;
    float x = r * cos(theta); // 極座標をデカルト座標に変換
    float y = r * sin(theta); // 極座標をデカルト座標に変換
    ellipse(x, y, 20, 20); // 変換されたデカルト座標で円を描画
  }
}

まとめ

極座標系は、円周や回転に関連する問題を表現する際に特に有用です。極座標とデカルト座標は相互に変換可能であり、どちらの座標系を使用するかは、特定の問題や状況によって決まります。

>>Part.3へ続く

演習

演習1:

半径100、角度45度の極座標をデカルト座標に変換してその場所に半径10の円を描画してください。

演習2:

半径が50、100、150の3つの円を極座標系を使用して描画してください。

演習3:

角度θが0から360度の間で変化する際の、半径r=100の円周上の点をデカルト座標で描画してください。

演習4:

半径rが時間tに応じて変化する点を、極座標系を使用してアニメーション描画してください。

演習5:

極座標系で表現される螺旋を描画してください。

演習6:

極座標系を使用して、花びらのような図形を描画してください。

演習7:

異なる半径と角度を持つ複数の点を、極座標系を使用してランダムに描画してください。

演習8:

マウスの位置に応じて半径が変化する円を極座標系を使用して描画してください。

演習9:

極座標系で表現される正方形を描画してください。

演習10:

極座標系を使用して、中心から放射状に線を引いて太陽のような図形を描画してください。