Processingにおける回転・振動の実装 Part.4 波・振り子

Part.3に続いてProcessingによる回転・振動に関する表現の解説です。Part.4では波・振り子を取り扱います。

波の実装

Processingで波をコーディングするには、通常、三角関数（特にsin関数またはcos関数）を使用します。これらの関数を使用して、時間や空間において波の動きをシミュレートできます。以下は、Processingで水平方向に動く波を描画する基本的なコード例です。

波の基本パラメータ

振幅 (Amplitude): 波の高さ。波が中心ラインからどれだけ上下に動くかを決定します。
波数 (Wavelength): 一つの波が占める幅。小さいほど波は密になります。
周波数 (Frequency) / 角速度 (Angular Frequency): 波がどれだけ速く動くか。時間に対する波の速度を決定します。
位相 (Phase): 波の開始位置。波の位置を水平方向にシフトします。

波の描画の基本コード例

float amplitude = 50;  // 振幅
float wavelength = 100;  // 波長
float speed = 0.02;  // 波の速度

void setup() {
  size(800, 200);
}

void draw() {
  background(255);
  translate(0, height / 2);  // 描画の中心を画面の中央に移動
  stroke(50);
  
  // 各x位置における波のy位置を計算して描画
  for(float x = 0; x <= width; x += 0.5) {
    float angularFrequency = TWO_PI / wavelength;  // 角速度（波数）
    float phase = millis() * speed;  // 位相（時間経過による波の移動）
    float y = sin(x * angularFrequency + phase) * amplitude;  // y位置の計算
    point(x, y);  // 波の一部となる点を描画
  }
}

このコードは、sin関数を使用して、時間の経過とともに動く波を描画します。amplitudeで波の高さ、wavelengthで波の幅、speedで波の速度を調整できます。

振り子の実装

Processingで振り子をコーディングするには、物理の法則、特にニュートンの運動方程式と力の概念を基本にシミュレーションを行います。振り子は重力によって揺れ、その運動は三角関数を使って表現できます。

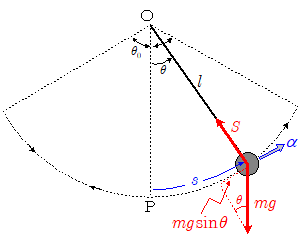
振り子のパラメータ

長さ (Length): 固定点から振り子の質量中心までの距離。
角度 (Angle): 垂直軸からの振り子の偏角。
重力 (Gravity): 重力加速度。

振り子のコーディング

以下は、Processingを使って基本的な振り子を描画するためのコード例です。

float angle = PI / 4; // 初期角度
float angleVel = 0.0; // 角速度
float angleAcc = 0.0; // 角加速度

float pendulumArmLength = 150.0; // 振り子の腕の長さ
float gravity = 0.4; // 重力加速度

void setup() {
  size(400, 400);
}

void draw() {
  background(255);

  // 角加速度を計算（重力と角度から）
  angleAcc = (-1 * gravity / pendulumArmLength) * sin(angle);

  // 位置、速度、加速度を更新
  angle += angleVel;
  angleVel += angleAcc;
  angleVel *= 0.99; // 摩擦による減速

  // 振り子の腕の位置を計算
  float x = pendulumArmLength * sin(angle);
  float y = pendulumArmLength * cos(angle);

  translate(width / 2, 200); // 振り子の固定点へ移動
  stroke(0);
  fill(127);
  line(0, 0, x, y); // 振り子の腕を描画
  ellipse(x, y, 20, 20); // 振り子のボブを描画
}

このコードは、与えられた初期角度から振り子を揺らします。重力、摩擦、初期角度を変えることで、振り子の動きを様々にシミュレートできます。

※振り子の角速度が -gravity/pendulumArmLengthとなる理由は以下などを参考にしてみてください。

>> Part.5へ続く

演習

演習1: 基本的な波の描画

Processingを使用して、基本的な正弦波を描画してください。振幅、波長、速度を変更して、その影響を観察してください。

演習2: 波の重ね合わせ

2つ以上の異なるパラメータを持つ正弦波を重ね合わせて描画し、結果の波形を観察してください。

演習3: 振り子の描画

基本的な振り子を描画してください。振り子の長さや初期角度を変更し、その影響を観察してください。

演習4: 重力の変更

振り子のコードで重力の値を変更し、その影響を観察してください。

演習5: 振幅変調

時間によって振幅が変わる正弦波を描画してください。例えば、振幅が徐々に大きくなる、または小さくなる波です。

演習6: マウスによる波の制御

マウスの位置に基づいて、波の速度や振幅を変更するコードを書いてください。

演習7: 振り子の列

複数の振り子を描画し、それらが互いに影響を与えるようにしてください。例えば、隣り合う振り子が互いに引き合うようにします。

演習8: 波の反射

画面の端で波が反射するように描画してください。つまり、波が画面の端に達すると、反対方向に動きます。

演習9: 外力による振り子の動き

マウスクリックやキーボードの入力で、振り子に外力が加わるようにしてください。これにより、振り子の動きがどのように変化するか観察してください。

演習10: 波形の可視化

異なる波形（正弦波、三角波、矩形波など）を描画し、それらの違いを観察してください。