Processingにおける回転・振動の実装 Part.1 角度と三角関数の基礎

Processingにおいて三角関数を応用することで、オブジェクトの回転や振動のアニメーションを作成することができます。Part.1では「角度と三角関数の基礎」について解説します。

Processingにおける角度の基礎

Processingでは、角度を取り扱う際に主に二つの単位が利用されます：度（degree）とラジアン（radian）。三角関数を利用する際や、オブジェクトを回転させる際などに、角度の取り扱いが必要となります。

1. ラジアンと度

ラジアン: 円周の長さと半径の長さの比率で定義されます。1ラジアンは、約57.296度です。
度: 1度は、円を360等分した1つ分の角度です。

2. 角度の変換

Processingでは、radians()とdegrees()関数を利用して、度とラジアンの間で角度を変換できます。

radians(角度): 度単位の角度をラジアン単位に変換します。
degrees(角度): ラジアン単位の角度を度単位に変換します。

3. オブジェクトの回転

rotate()関数を利用して、オブジェクトを回転させることができます。rotate()関数は、ラジアン単位で角度を受け取ります。

void setup() {
  size(200, 200);
}

void draw() {
  background(255);
  translate(width / 2, height / 2); // 座標系の中心を移動
  rotate(radians(frameCount)); // frameCountをラジアンに変換して回転
  rectMode(CENTER);
  rect(0, 0, 50, 50);
}

※translate関数は画面の原点の位置を指定したx, yの値だけずらします。この例の場合だと、左上にあった原点を画面中央に移動させています。

※rotate関数は原点の周りに時計回りに座標を回転させます。

4. 三角関数の利用

sin(), cos(), tan()などの三角関数は、ラジアン単位で角度を受け取ります。

float angle = radians(45); // 45度をラジアンに変換
float x = cos(angle) * 100; // 45度の余弦
float y = sin(angle) * 100; // 45度の正弦

※初めからラジアンの単位を用いるなら angle = PI/4 とするのと同じです。

なぜラジアンという単位を用いるのか？

ラジアンは、角度の単位として度数（度）と並んで用いられますが、数学や物理学、コンピュータサイエンスの多くの分野で、度数よりもラジアンが好まれます。これにはいくつかの理由があります。そもそも1周の角度が360度という数字は恣意的に決めた数字なので、数学的な必然性がないものでした。

1. 自然な単位:

ラジアンは、円周の長さと半径の長さの比として定義されるため、三角関数や幾何学の問題を扱う際に自然な単位となります。これは、円や周期的な動き、振動などを扱う際に特に便利です。

※単位円(半径1の円)の円周は2πですが、単位円の円弧の長さをそのまま角度の単位として使用していると考えても良いです。（円のサイズが大きくなっても角度が変わらないように定義としては円弧/半径で定義しています）

2. 微分と積分の単純化:

ラジアンを使用すると、三角関数の微分と積分が単純化されます。例えば、sin(x)の導関数はcos(x)となりますが、これはxがラジアンで測定されている場合のみ成り立ちます。度で測定した場合、導関数には変換係数が必要となります。

3. 計算の効率:

コンピュータサイエンスにおいて、ラジアンは度数よりも効率的に計算できます。多くのプログラム言語やライブラリは、三角関数を計算する際にラジアンを入力として期待します。このため、度をラジアンに変換する手間を省くことができます。

4. 一般性:

ラジアンは単位のない純粋な数値(比)であるため、単位間の変換なしに多くの数学的表現ができます。これにより、公式や計算が一般性を保ち、よりシンプルになります。

三角関数の基礎

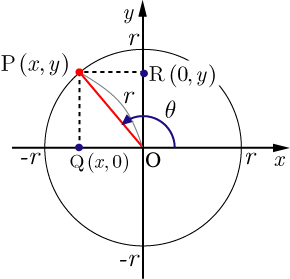
ここでは詳細まで解説できませんが、三角関数は単位円周上の任意の点におけるx座標, y座標のとして定義できます。

1. 正弦関数（Sine Function）: sin

定義: 直角三角形において、対角線の辺の長さ（対辺）を斜辺の長さで割ったもの。図ではsinθ = y/r。
単位円での表現: 半径1の単位円において、ある角度に対応する点のy座標。

2. 余弦関数（Cosine Function）: cos⁡

定義: 直角三角形において、隣接辺の長さを斜辺の長さで割ったもの。図ではcosθ = x/r。
単位円での表現: 半径1の単位円において、ある角度に対応する点のx座標。

3. 正接関数（Tangent Function）: tan⁡

定義: 直角三角形において、対辺の長さを隣接辺の長さで割ったもの。
表現: tan θ =sinθ / cosθ

>> Part.2へ続く